1. Write the sentence as an inequality.
The length r of a rope should be atleast 5 inches.
Plsss help!

Answers
Answer:
r <= 5
Step-by-step explanation:
I don't think it requires an explanation.
Related Questions
a data set consists of the data given below plus one more data point. when the additional point is included in the data set the sample mean of the resulting data set is 26.5. what is the value of the additional data point?23, 28, 20, 33, 42, 12, 19, 50, 36, 25, 19
Answers
The value of the additional data point is 36
To find the value of the additional data point, we can use the concept of the sample mean.
Given the data set: 23, 28, 20, 33, 42, 12, 19, 50, 36, 25, 19.
The sample mean of this data set is 26.5.
To find the value of the additional data point, we can use the formula for the sample mean:
(sample mean) = (sum of all data points) / (number of data points)
In this case, we have 11 data points in the original data set. Let's denote the value of the additional data point as x.
Therefore, we can set up the equation:
26.5 = (23 + 28 + 20 + 33 + 42 + 12 + 19 + 50 + 36 + 25 + 19 + x) / 12
Multiplying both sides of the equation by 12 to eliminate the fraction, we have:
318 = 282 + x
Subtracting 282 from both sides of the equation, we find:
x = 318 - 282
x = 36
Know more about sample mean here;
https://brainly.com/question/33323852
#SPJ11
.
What is the solution for -4x - 10 ≤ 2?
Answers
Answer:
x>=-3
Step-by-step explanation:
-4x-10<=2
-4x<=2+10
-4x<=12
x<=12/-4
x<=-3
x>=-3
An 6 inch tall can of soda can hold 150π cubic cm. What is the radius of the top?
Answers
9514 1404 393
Answer:
3.14 cm ≈ 1.235 in
Step-by-step explanation:
The formula for the volume of a cylinder is ...
V = πr²h
Solving for r, we find ...
r = √(V/(πh))
For the given values, the radius is ...
\(r=\sqrt{\dfrac{150\pi\text{ cm$^3$}}{\pi(6\text{ in})(2.54\text{ cm/in})}}=\sqrt{\dfrac{25}{2.54}}\text{ cm}\approx\boxed{3.14\text{ cm}}\)
Quadrilateral BASE is located at B (3, 4), A (-2, 3), S (4, 0), and E (-2, 5). BASE was dilated with a scale factor of 5 to create B’A’S’E’. Where is A’ located? Group of answer choices
A. (-10, 15)
B. (5, 5)
C. (15, 12)
D. (10, 15)
will give brainliest
Answers
The location of the point A' after dilation is; A'(-10, 15)
What is the result of dilation transformation?We are given that the Quadrilateral BASE is located at the following coordinates;
B(3, 4), A(-2, 3), S(4, 0), and E(-2, 5).
Now, if it is dilated by a scale factor of, it means that each of the coordinates values would be multiplied by 5 to get the new coordinates as;
B'(15, 20), A'(-10, 15), S'(20, 0), and E'(-10, 25).
Thus, we can conclude that the location of the point A' after dilation is; A'(-10, 15)
Read more about Dilation Transformation at; https://brainly.com/question/10253650
#SPJ1
What is the slope and y-intercept of the graph?
(2.1)
(-1.4)
Answers
Answer:
The slope is -1
Step-by-step explanation:
Use the formula m=y2-y1/x2-x1
A) describe a convenience sampleB) best describe a random sampleC) best describe a systemic sample
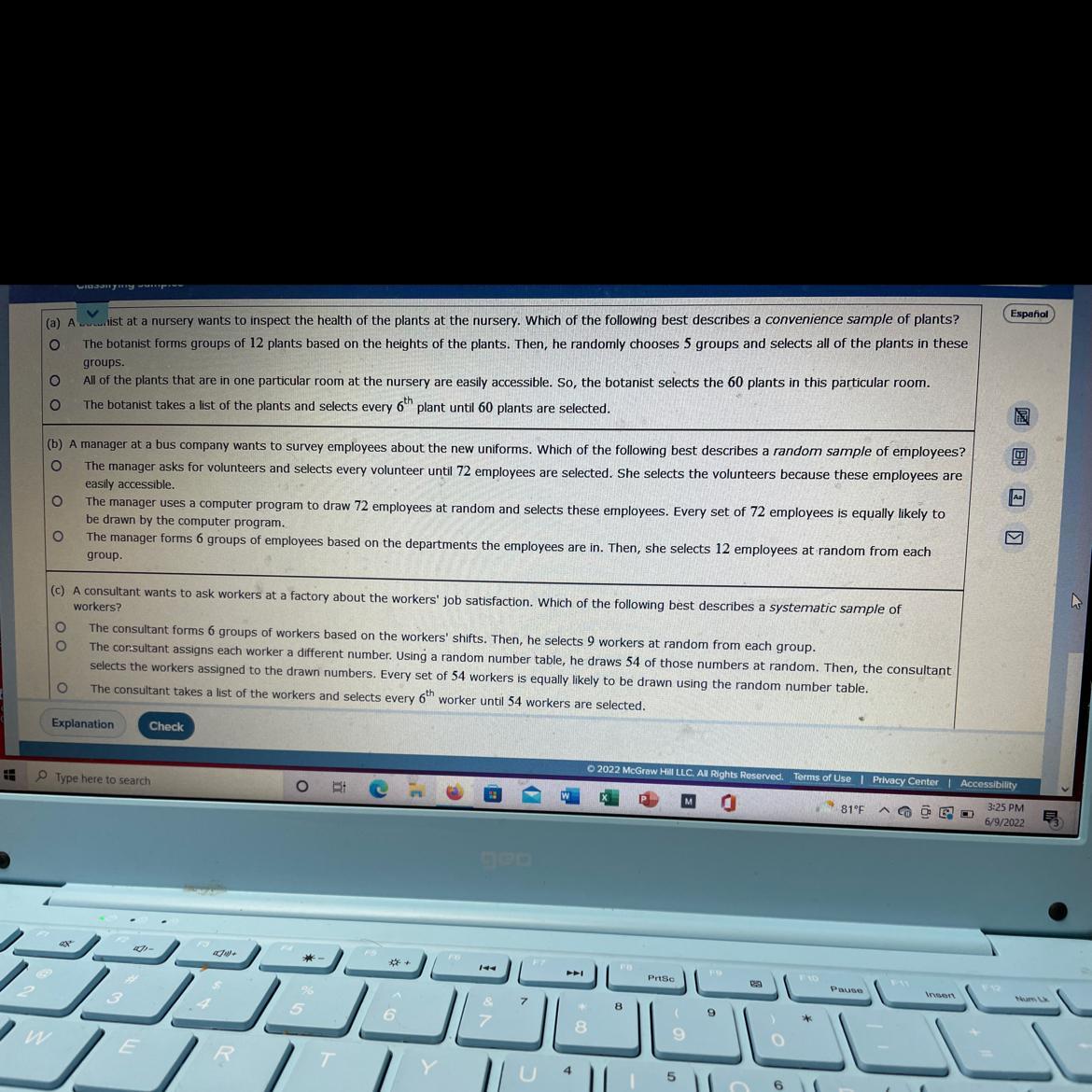
Answers
The Solution:
The correct answers are ticked in the picture below:
Therefore, the correct answers are:
[ option 2 ]
[ option 2 ]
[ option 3 ]

Is 499.50 great than or less than 499.05?
Answers
Answer:
greater
Step-by-step explanation:
Please solve in detail as much as you can. Discrete
Mathematics. Thank you.
Determine the coefficient of \[ w x^{3} y^{2} z^{2} \quad \text { in } \quad(2 w-x+y-2 z)^{8} \]
Answers
The coefficient of \(w x^{3} y^{2} z^{2}\) in \((2 w-x+y-2 z)^{8}\) is determined to be 560 using the multinomial coefficient formula.
To determine the coefficient of \(w x^{3} y^{2} z^{2}\) in \((2 w-x+y-2 z)^{8}\), we can use the binomial theorem.
According to the binomial theorem, the coefficient of a specific term in the expansion of \((a+b)^n\) is given by the multinomial coefficient \(\binom{n}{k_1, k_2, \ldots, k_m}\), where \(n\) is the exponent, and \(k_1, k_2, \ldots, k_m\) are the powers of each variable in the term.
In this case, we have the term \(w x^{3} y^{2} z^{2}\), where \(w\) has an exponent of 1, \(x\) has an exponent of 3, \(y\) has an exponent of 2, and \(z\) has an exponent of 2.
Using the multinomial coefficient formula, we can calculate the coefficient as follows:
\(\binom{8}{1, 3, 2, 2} = \frac{8!}{1! \cdot 3! \cdot 2! \cdot 2!}\)
Evaluating this expression gives us the coefficient of \(w x^{3} y^{2} z^{2}\) in \((2 w-x+y-2 z)^{8}\).
Simplifying the calculation, we have:
\(\binom{8}{1, 3, 2, 2} = \frac{8 \cdot 7 \cdot 6 \cdot 5}{1 \cdot 3 \cdot 2 \cdot 2} = 560\)
Therefore, the coefficient of \(w x^{3} y^{2} z^{2}\) in \((2 w-x+y-2 z)^{8}\) is 560.
Learn more about Coefficient click here :brainly.com/question/9242735
#SPJ1
describe in simple terms the convex hull of the set of special orthogonal matrices in r 3 : so(3) = {u ∈ r 3×3 |u >u = i, detu = 1}.
Answers
The convex hull of the set of special orthogonal matrices in R3 (denoted by SO(3)) is the smallest convex shape that contains all the matrices in SO(3).
In simpler terms, it is the shape that you would get if you took all the matrices in SO(3) and stretched and molded them until they formed a solid 3D shape. The matrices in SO(3) are special because they are orthogonal (meaning their columns are perpendicular to each other) and have a determinant of 1.
To know more about matrices visit:
https://brainly.com/question/30646566
#SPJ11
The convex hull of the set of special orthogonal matrices in ℝ³, denoted SO(3), can be described as the smallest convex shape that contains all the special orthogonal matrices in ℝ³.
What is a matrix?
A matrix is a rectangular array of numbers or elements arranged in rows and columns. It is a fundamental mathematical object used in various fields such as linear algebra, computer science, and physics.
To understand this concept in simple terms, we can think of special orthogonal matrices as matrices that represent rotations in three-dimensional space. They have special properties, such as having a determinant of 1 and being orthogonal (i.e., their columns and rows are orthogonal unit vectors).
The convex hull of SO(3) consists of all the possible rotations that can be achieved by combining different rotations about different axes. This convex hull forms a solid shape that encloses all the special orthogonal matrices.
In geometric terms, the convex hull of SO(3) can be visualized as a three-dimensional shape resembling a solid ball or sphere. It represents all the possible rotations in three-dimensional space that can be obtained by combining rotations about different axes.
To know more about orthogonal matrices, refer here:
https://brainly.com/question/30638339
#SPJ4
BRAINLIST!!!!!!!!!!!!!
FIND THE AREA OF THE COMPOSITE FIGURE

Answers
David cuts 4 pieces of wood for a birdhouse. When he is done, he realizes that each piece is 2 1/3 inches too short. How does the total length of the pieces compare to what their total length should have been? Explain or show how you got your answer
Answers
Answer:
Total Length is 9 1/3 inches shorter Than the required length
Step-by-step explanation:
Number of wood pieces cut = 4
Each piece is 2 1/3 inches too short
Total shortage in length :
Number of pieces * shortage per piece
4 * 2 1/3
4 * 7/3
= 28/3 inches = 9 1/3 inches
Hence, The total length of the wood is 9 1/3 inches shorter than the actual or required length of the wood.
which expression shows the relationship between the ratios 1 to 2 and 3 to 6
Answers
Answer:help me
Step-by-step explanation:
Answer:
x3
Step-by-step explanation:
Of a total of 6,000.00, part was invested at a simple interest rate of 8% and part at 7% if the total interest income for one year was $46.00, how many was invested at 7%
Answers
Answer: Ok so first 0.05(6000 - x) + 0.07x = 372
300 - 0.05x + 0.07x = 372
300 + 0.02x = 372
0.02x = 72
x = 3600
He invested $3600 at 7% and $2400 at 5%.
Hope this helps have a bless day❤️Step-by-step explanation:
Answer:
Step-by-step explanation:
I think you had a typo where interest should be 460 not 46 because even if the whole 6000 were invested at 7% he would have earned $420 in interest. Also if total investment was switched from 6000 to 600 the 46 in interest would work.
.07x+.08(6000-x)=460
.07x-.08x+480=460
-.01x+480=460
-.01x=-20
x=$2000
which is easy enough to check
2000(.07)+4000(.08)=$460
2 circles labeled Set A and Set B overlap. Set A contains 1, set B contains 3, and the overlap of the 2 circles contains 2. The number 4 is outside of the circles. On the Venn diagram, which region(s) represent the intersection of Set A and Set B (Aâ©B)? II I and III I, II, and III I, II, III, and IV.
Answers
The intersection of sets is the point that represents the common point of multiple sets.
The region that represents the intersection of sets A and B is region II.
From the question, we understand that sets A and B have a common set element at II.
This means that region II is the intersection of both sets.
Hence, the region that represents the intersection of sets A and B is II.
Read more about set intersection at:
https://brainly.com/question/6779867

Answer:
II is the answer
Step-by-step explanation:
Edge 2022
suppose that the xis are independent with each one having a normal distribution. what is the probability that the total volume shipped is more than 100,000 ft3 ?
Answers
We can use the properties of the normal distribution to calculate the probability that the total volume shipped is more than 100,000 ft3.
Assuming that the xis are independent with each one having a normal distribution, the total volume shipped can be modeled as the sum of these individual normal distributions. Since the sum of independent normal distributions is also a normal distribution, we can use the properties of the normal distribution to calculate the probability that the total volume shipped is more than 100,000 ft3.
To do this, we need to find the mean and variance of the sum of the xis. The mean of the sum is simply the sum of the means of the individual distributions, while the variance of the sum is the sum of the variances of the individual distributions.
Once we have the mean and variance of the sum, we can standardize the distribution and use a normal probability table or calculator to find the probability that the total volume shipped is more than 100,000 ft3.
In general, the probability of the sum of independent normal distributions exceeding a certain value depends on the number of distributions being summed, their means and variances, and the level of significance chosen for the test. Therefore, we need to specify these parameters to calculate the desired probability.
Learn more about probability brainly.com/question/30034780
#SPJ11
Find the sum of the following series. Round to the nearest hundredth if
necessary
5 + 10 + 20 + ... + 163840
Sum of a finite geometric series:
ai
Sn
di — airon
1 - 1
Answers
Answer:
327675
Step-by-step explanation:
the formula of the series is:
16
∑5*2^(n-1)
n=1
the formula for the sum of a geometric series is:
Sn=a(1-r^n)/(1-r)
plug in the values from above
n=16 a=5 and r=2 (values from the geometric function) so
Sn=5(1-2^16)/(1-2)
Sn=327675
When she enters college, Simone puts $500 in a savings account
that earns 3.5% simple interest yearly. At the end of the 4 years,
how much money will be in the account?
Answers
At the end of the 4 years, there will be $548 in Simone's savings account.The simple interest rate of 3.5% per year allows her initial investment of $500 to grow by $70 over the course of four years.
To calculate the amount of money in the account at the end of 4 years, we can use the formula for simple interest:
Interest = Principal * Rate * Time
Given that Simone initially puts $500 in the account and the interest rate is 3.5% (or 0.035) per year, we can calculate the interest earned in 4 years as follows:
Interest = $500 * 0.035 * 4 = $70
Adding the interest to the initial principal, we get the final amount in the account:
Final amount = Principal + Interest = $500 + $70 = $570
Therefore, at the end of 4 years, there will be $570 in Simone's savings account.
Simone will have $570 in her savings account at the end of the 4-year period. The simple interest rate of 3.5% per year allows her initial investment of $500 to grow by $70 over the course of four years.
To know more about simple interest follow the link:
https://brainly.com/question/8100492
#SPJ11
A rectangular photograph is 8 cm wide and 12 cm long. The photograph is enlarged by increasing the length and width byan equal amount in order to double its area. What are the dimensions of the new photograph?
a. 12 cm by 16 cm
b. 16 cm by 24 cm
C. 20 cm by 30 cm
d. 48 cm by 72 cm
Answers
Answer:
16 cm by 24 cm
Step-by-step explanation:
Well if you want an equal amount you will have to multiply both numbers by the same thing. I used 2 and 16 cm by 24 cm would be your answer.
The dimensions of the new photograph is b. 16 cm by 24 cm.
What is the area of the rectangle?The area of the rectangle is the product of the length and width of a given rectangle.
The area of the rectangle = length × Width
A rectangular photograph is 8 cm wide and 12 cm long.
The original area is
8 x 12 = 96
The photograph is enlarged by increasing the length and width by an equal amount in order to double its area.
The new area is 96 x 2 = 192
So the dimensions are b. 16 cm by 24 cm.
Learn more about the area;
https://brainly.com/question/1658516
#SPJ2
The weather in Columbus is either good, indifferent, or bad on any given day. If the weather is good today, there is a 60% chance it will be good tomorrow, a 30% chance it will be indifferent, and a 10% chance it will be bad. If the weather is indifferent today, there is a 50% chance it will be good tomorrow, and a 20% chance it will be indifferent. Finally, if the weather is bad today, there is a 40% chance it will be good tomorrow and a 30% chance it will be indifferent. The stochastic matrix for this situation is shown to the right. In the long run, how likely is it for the weather in Columbus to be indifferent on a given day? 0.6 0.5 04 P-1 0.3 0.2 0.3 0.1 0.3 0.3 In the long run, how likely is it for the weather in Columbus to be indifferent on a given day?
Answers
In the long run, the likelihood of indifferent weather in Columbus on a given day is approximately 29.3%.
To find the long-term likelihood of indifferent weather in Columbus, we need to find the steady-state probabilities of the stochastic matrix provided. The matrix is given as:
P = | 0.6 0.5 0.4 |
| 0.3 0.2 0.3 |
| 0.1 0.3 0.3 |
1. First, find the transpose of the matrix P:
P^T = | 0.6 0.3 0.1 |
| 0.5 0.2 0.3 |
| 0.4 0.3 0.3 |
2. Next, subtract the identity matrix I from the transpose of P:
P^T - I = | -0.4 0.3 0.1 |
| 0.5 -0.8 0.3 |
| 0.4 0.3 -0.7 |
3. To find the steady-state probabilities, we need to solve the system of linear equations:
(-0.4)x + 0.3y + 0.1z = 0
0.5x - 0.8y + 0.3z = 0
We also have an additional constraint since the sum of probabilities must equal 1:
x + y + z = 1
4. Solve this system of linear equations using any method (substitution, elimination, or matrix method). The resulting probabilities are:
x = 0.432 (good weather probability)
y = 0.293 (indifferent weather probability)
z = 0.275 (bad weather probability)
To learn more about likelihood, refer here:
https://brainly.com/question/28602693#
#SPJ11
5. What values of A, B and C will make the following two planes be parallel? What values will make them be perpendicular? T₁ = 2x - 5y + z-4 = 0 and 2 = Ax+By+ Cz + 10 = 0 [4 marks]
Answers
The values of A, B, and C that make the two planes parallel are: A = (5B - C)/2and5B - 3C = |N₁||N₂|/2 and The values of A, B, and C that make the two planes perpendicular are: A = (5B - C)/2and5B - 3C = 0.
Let's have a look at the planes. They are:
T₁ = 2x - 5y + z - 4 = 0 and T₂ = Ax + By + Cz + 10 = 0
Now we will try to solve the question using the concepts of vector and normal to the plane.
The vector and normal to the plane can be defined as follows:
A plane is a 2-dimensional surface that is defined by three points.
A normal is a vector that is perpendicular to the plane.
A vector is a quantity that has both magnitude and direction. Let's calculate the normal to both planes using the coefficients of x, y, and z in the equation of the planes.
The equation of the normal to a plane is given by:
N = ai + bj + ck where a, b, and c are the coefficients of x, y, and z in the equation of the plane.
Let's first find the normal to T₁.
The coefficients of x, y, and z are 2, -5, and 1, respectively.
Therefore, the normal to T₁ is given by:
N₁ = 2i - 5j + k
Now let's find the normal to T₂. The coefficients of x, y, and z are A, B, and C, respectively. Therefore, the normal to T₂ is given by:
N₂ = Ai + Bj + Ck
Now that we have found the normals to the two planes, we can determine if they are parallel or perpendicular based on the dot product of the two normals.
The dot product of two vectors is given by:
A.B = |A||B|cosθwhere A and B are two vectors, |A| and |B| are their magnitudes, and θ is the angle between them.
If the dot product of the two normals is zero, then the planes are perpendicular. If the dot product of the two normals is not zero, then the planes are parallel. In this case, we need to find the values of A, B, and C that make the two planes parallel or perpendicular.
Now let's find the dot product of the two normals:
N₁.N₂ = 2A - 5B + C
If the two planes are parallel, then their normals are parallel, which means that the dot product of the two normals is equal to the product of their magnitudes.
Therefore:
N₁.N₂ = |N₁||N₂|I
f the two planes are perpendicular, then their normals are perpendicular, which means that the dot product of the two normals is zero.
Therefore:
N₁.N₂ = 0
Now let's find the values of A, B, and C that make the two planes parallel or perpendicular. If the two planes are parallel, then their normals are parallel.
Therefore, the dot product of the two normals is equal to the product of their magnitudes.
Therefore:
2A - 5B + C = |N₁||N₂|I
f the two planes are perpendicular, then their normals are perpendicular.
Therefore, the dot product of the two normals is zero.
Therefore:2A - 5B + C = 0
Now let's solve the two equations for A, B, and C.
2A - 5B + C = |N₁||N₂|2A - 5B + C = 0A = (5B - C)/2
Substituting this value of A into the equation 2A - 5B + C = |N₁||N₂|, we get:
5B - 3C = |N₁||N₂|/2
Therefore, the values of A, B, and C that make the two planes parallel are:
A = (5B - C)/2and5B - 3C = |N₁||N₂|/2
The values of A, B, and C that make the two planes perpendicular are:
A = (5B - C)/2and5B - 3C = 0
To know more about parallel visit:
https://brainly.com/question/17405097
#SPJ11
Dried cranberries cost £9.20 per kilogram. Calculate the cost of 650g of dried cranberries
Answers
Answer:
£5.98
Step-by-step explanation:
Using the conversion
1 Kg = 1000g, then
650g = 650 ÷ 1000 = 0.65 Kg
Thus the cost of 650g = 0.65 × £9.20 = £5.98
The endpoints of a side of rectangle ABCD in the coordinate plane are at A(2, 7) and
B(4, 1). Find the equation of the line that contains the given segment.
The line segment is AB.
The equation is y =
Answers
Answer:
ole los caracoles con mi amiga
Step-by-step explanation:
jeja
find the radian measure of an angle at the center of a circle with radius 77.0 cm that intercepts an arc length of 128 cm
Answers
The radian measure of the angle at the center of the circle is approximately 1.6623 radians.
We are given that the radius of the circle is 77.0 cm and the length of the intercepted arc is 128 cm. We need to find the radian measure of the angle at the center of the circle.
To solve this problem, we use the formula relating the angle at the center of a circle, the radius of the circle, and the arc length intercepted by the angle.
The formula is given byθ = s/rwhereθ = angle at the center of the circle in radians s = arc length intercepted by the angle r = radius of the circle Substituting the given values, we getθ = 128/77.0 = 1.6623 radians (rounded to four decimal places)
Therefore, the radian measure of the angle at the center of the circle is approximately 1.6623 radians.
For more such questions on radian measure
https://brainly.com/question/19758686
#SPJ8
Use the graph of f '(x) below to find the x values of the relative maximum on the graph of f(x):
Answers
The relative maximum on the graph of f(x) is at x = 1
How to determine the relative maximumThe complete question is added as an attachment
The critical points of a function f(x) are the values of x for which:
f"(x) > 0 is minimumf"(x) < 0 is maximumf"(x) = 0 is either minimum or maximumIn this graph, the critical points are: .
x = 0, x = 1 and x = 2
For each of the critical points, we have
At x = 0, f'(x) is increasing, so x is a minimum.At x = 1, f'(x) is decreasing so x = 0 is a maximum.At x = 2, f'(x) is increasing, so x = 2 is a minimum.Read more about derivative at
brainly.com/question/2256078
#SPJ1

An economist estimates a sample production function model in which firm output in a particular industry depends on the amount of labor seed by a Ann Based on her estimates, emplaying another workers predicted to lead to a 32 percent increase in output to ani, denote the amount output produced and the number of workers employed by the th firm, then which of the following regressions is the economies entimated region O a Can't say it could be any of the regressions.
a. cant say : it could be any of the regressions
b. Q1 - 10.74 + 3.2 Li
c. log(Q1) = 10.74 + 0.032 Li
d. log(Q1) = 10.74 + 0.32 log(Li)
Answers
Based on the given information, the regression that represents the estimated production function model for firm output in the industry is:
c. log(Q1) = 10.74 + 0.032 Li
The regression equation in option c represents a logarithmic relationship between the output (Q1) and the number of workers employed (Li). Taking the logarithm of the output variable allows for a more flexible functional form and captures potential diminishing returns to labor.
In the regression equation, the constant term (10.74) represents the intercept or the level of output when the number of workers is zero. The coefficient of 0.032 (0.032 Li) indicates the relationship between the logarithm of output and the number of workers employed.
Since the question states that employing another worker leads to a 32 percent increase in output, this aligns with the coefficient of 0.032 in the regression equation. It suggests that a 1 percent increase in the number of workers (Li) leads to a 0.032 percent increase in output, which is equivalent to a 32 percent increase.
Therefore, the regression equation in option c best represents the estimated production function model in this scenario.
Learn more about function here: brainly.com/question/30660139
#SPJ11
what sports do you play?
Answers
Answer:
football
Step-by-step explanation:
also known as soccer
The goal of building one-to-many relationships between tables is to minimize _____ data. A. misspelled B. rarely used C. numeric D. redundant
Answers
The goal of building one-to-many relationships between tables is to minimize redundant data.
Data redundancy is a regular occurrence in many businesses and occurs when an identical piece of data is stored in two or more different locations. As more businesses switch from using segregated data to a central repository, they discover that their database is full of inconsistent duplicates of the same entry. Understanding how to effectively manage and track data redundancy can help your business avoid long-term inconsistency problems, even though it can be difficult to reconcile — or even benefit from — redundant data entries.
learn more about redundancy data ,
https://brainly.com/question/13438926
#SPJ11
The goal of building one-to-many relationships between tables is to minimize redundant data.
Redundant data refers to data that is duplicated across multiple tables, which can lead to data inconsistencies and
increase the amount of storage space required.
By creating one-to-many relationships between tables, data is only stored once in the database, and each instance of
the data in other tables refer back to the original source, reducing the need for redundant data storage.
Therefore, The goal of building one-to-many relationships between tables is to minimize redundant data.
for such more questions on redundant data
https://brainly.com/question/30020503
#SPJ11
ryan drove 260 miles using 12 gallons of gas. at this rate, how many gallons of gas would he need to drive 286 miles?
Answers
The gallons of gas required by Ryan to travel 286 miles is 13.2 gallons.
Define the term inversely proportional?When two parameters are related, an inverse connection exists, where the value about one parameter usually falls as the value of other parameter rises. It's frequently referred to as a bad relationship. When one quantity increases or declines, the other quantity also rises or falls in direct proportion. On the other hand, in indirect and inverse proportion, if such quantity rises, the other one falls, and vice versa.As the stated question;
Total gallon of gas used to drive the 260 miles = 12 gallons
Let 'x' be the gallon of gas used to drive the 286 miles.
Then, bu using the proportion
12 / 260 = x / 286
Thus,
x = 286 x 12 / 260
x = 13.2 gallons
Thus, the amount of gas required by Ryan to travel 286 miles is 13.2 gallons.
To know more about the inversely proportional, here
https://brainly.com/question/1266676
#SPJ4
Pls help me!!!!!!!!!!!

Answers
Answer:
1) y-4+1(x-5)
Step-by-step explanation:
With point-slope form, you just have to substitue the information that is given to you into the generic formula.
y-y1= m(x-x1)
so the y1 is the y value of the point that is given to you and x1 is the x value of the point that is given to you
m is the slope (also given)
and x and y just stay the same; x &y
Write an equation in slope-intercept form of the line that passes through the points (4,1) and (8,2)
Answers
Answer:
y=1/4x
Step-by-step explanation: in image below
